Electric field due to a charge at a point in space may be defined as the force that a unit positive charge would experience if placed at that point.
Thus the electric field produced by a charge Q at a point $\vec{r}$ will be
\[\vec{E}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{\left | \vec{r} \right |^{2}}\hat{r}\]
 |
| Direction of Electric field due to +ve charge |
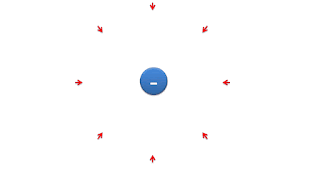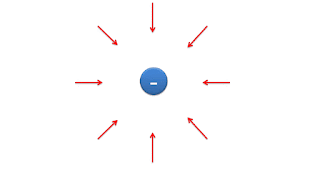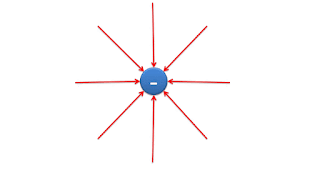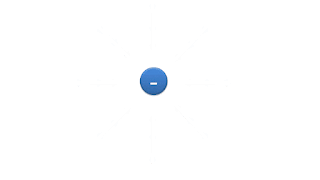 |
| Direction of Electric field due to -ve charge |
Electric Field Lines :
When a unit charge is placed in
the electric field of another charged particle, it will experience a force. The direction of this force can be represented by the
imaginary lines. These imaginary lines are called electric lines of force.
Electric lines of force are also called as electric field lines. The concept of
electric lines of forces was introduced by Michael Faraday in 1837.
Properties of electric lines of
force -
- The electric lines of force start from a positive charge and ends on a negative charge.
- The electric lines of force always enter or leave the charged surface normally.
- Electric lines of force can never intersect each other.
- The electric lines of force cannot pass through a conductor.
- When two opposite charges are placed close to each other, the electric lines of force present between them will become shorten in length.
- When two like charges are placed closer to each other, the electric lines of force present between them will become enlarged in length.
Electric Field due to System of Charges
In a system of charges $q_{1}$, $q_{2}$, ....., $q_{n}$ with position vectors $\vec{r_{1}}$, $\vec{r_{2}}$, ......, $\vec{r_{n}}$ relative to some origin O. The resultant electric field at O will be $\vec{E}=\vec{E_{1}}+\vec{E_{2}}+......+\vec{E_{n}}$
\[\Rightarrow \vec{E}=\frac{1}{4\pi \epsilon _{0}}\frac{q_{1}}{\left | \vec{r}_{1} \right |^{2}}\hat{r_{1}}+\frac{1}{4\pi \epsilon _{0}}\frac{q_{2}}{\left | \vec{r}_{2} \right |^{2}}\hat{r_{2}}+.....+\frac{1}{4\pi \epsilon _{0}}\frac{q_{n}}{\left | \vec{r}_{n} \right |^{2}}\hat{r_{n}}\]
In a system of charges $q_{1}$, $q_{2}$, ....., $q_{n}$ with position vectors $\vec{r_{1}}$, $\vec{r_{2}}$, ......, $\vec{r_{n}}$ relative to some origin O. The resultant electric field at O will be $\vec{E}=\vec{E_{1}}+\vec{E_{2}}+......+\vec{E_{n}}$
\[\Rightarrow \vec{E}=\frac{1}{4\pi \epsilon _{0}}\frac{q_{1}}{\left | \vec{r}_{1} \right |^{2}}\hat{r_{1}}+\frac{1}{4\pi \epsilon _{0}}\frac{q_{2}}{\left | \vec{r}_{2} \right |^{2}}\hat{r_{2}}+.....+\frac{1}{4\pi \epsilon _{0}}\frac{q_{n}}{\left | \vec{r}_{n} \right |^{2}}\hat{r_{n}}\]
\[\therefore \vec{E}=\frac{1}{4\pi \epsilon _{0}}\sum_{j=1}^{n}\frac{q_{j}}{\left | \vec{r}_{j} \right |^{2}}\hat{r_{j}}\]